一、解题策略

　　（1）弄清楚复合场的组成，一般有磁场、电场的复合，磁场、重力场的复合，磁场、电场、重力场三者的复合.

　　（2）正确进行受力分析，除重力、弹力、摩擦力外要特别注意静电力和磁场力的分析.

　　（3）确定带电粒子的运动状态，注意运动情况和受力情况的结合.

　　（4）对于粒子连续通过几个不同场的问题，要分阶段进行处理，转折点的速度往往成为解题的突破口.

　　（5）画出粒子运动轨迹，灵活选择不同的运动规律.

　　①当带电粒子在复合场中做匀速直线运动时，根据受力平衡列方程求解.

　　②当带电粒子在复合场中做匀速圆周运动时，应用牛顿第二定律结合圆周运动规律求解.

　　③当带电粒子做复杂曲线运动时，一般用动能定理或能量守恒定律求解.

　　④对于临界问题，注意挖掘隐含条件.

　　二、特别提示

　　在解决复合场问题时，明确带电粒子的重力是否需要考虑是正确而快速解题的前提，对于复合场中是否考虑粒子重力，常有以下三种情况：

　　1.对于微观粒子，如电子、质子、离子等，因为其重力一般情况下与静电力或磁场力相比太小，可以忽略；而对于一些实际物体，如带电小球、液滴、金属块等，一般应当考虑其重力.

　　2.在题目中有明确说明是否要考虑重力的，这种情况比较正规，也比较简单.

　　3.不能直接判断是否要考虑重力的，在进行受力分析与运动分析时，要由分析结果确定是否要考虑重力.

　　三、常用结论

　　①带电微粒在重力场、电场和磁场三种场共同作用下做直线运动时，其所受的三个场力的合力一定为零，且为匀速直线运动.

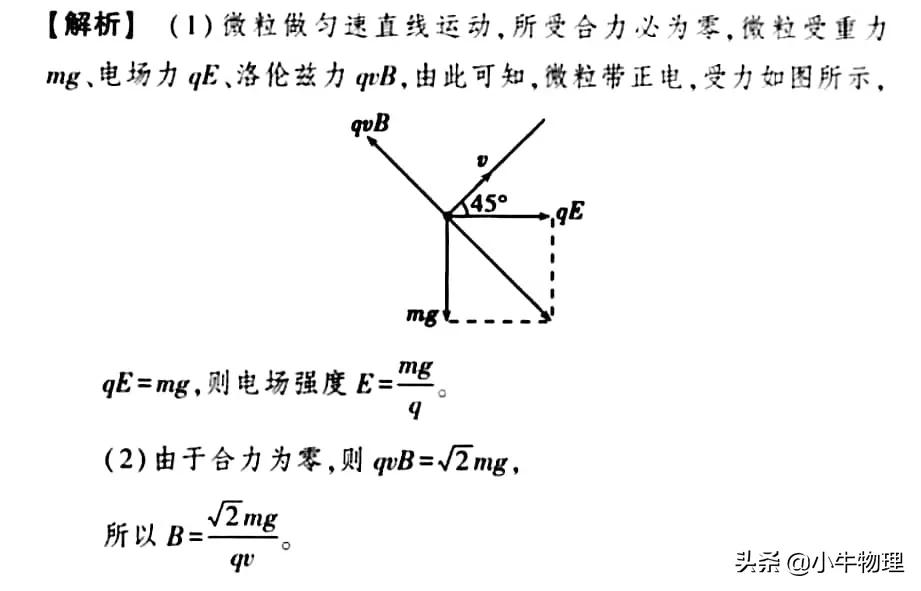
　　例题：质量为m，带电量为q的微粒，以速度v与水平方向成45°角进入匀强电场和匀强磁场同时存在的空间，如图所示，微粒在电场、磁场、重力场的共同作用下做匀速直线运动，求：

　　

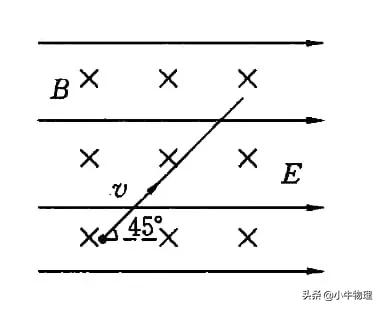
　　（1）电场强度的大小，该带电粒子带何种电荷.

　　（2）磁感应强度的大小.

　　

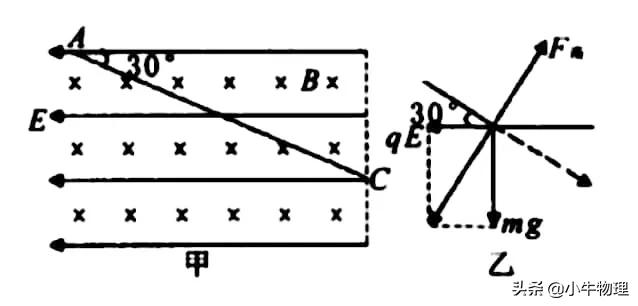
　　例题：如图，在地面附近的竖直面内，有沿水平方向垂直纸面向里的匀强磁场磁感应强度大小为B同时存在着水平向左的匀强电场场强大小为E，一个油滴在此复合场中始终沿与水平方向成30°角的方向斜向下做直线运动其运动轨迹如图中实线，下列说法正确的是（AD）

　　

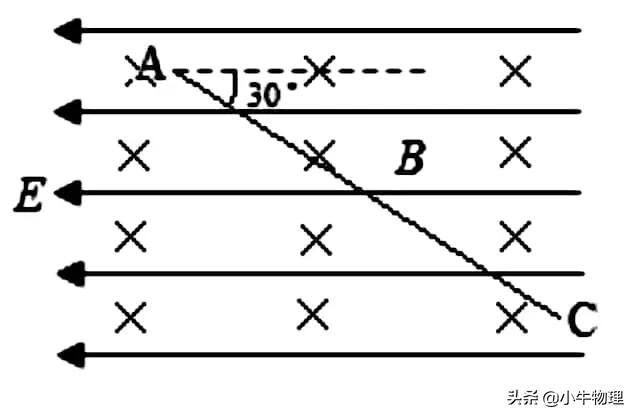
　　A.油滴一定带正电

　　B.油滴一定带负电

　　C.油滴一定做匀加速直线运动

　　D.油滴一定做匀速直线运动

　　

　　②带电粒子在复合场中做匀速圆周运动时，必定有其它力与恒定的重力相抵消，以确保合力大小不变，方向时刻指向圆心。一般情况下重力恰好与电场力平衡，洛伦兹力充当向心力，粒子在竖直平面内做圆周运动这类题，它的隐含条件就是重力恰好与电场力平衡。

　　例题：场强为E的匀强电场和磁感强度为B的匀强磁场正交，如图所示，一质量为的带电粒子，在垂直于磁场方向的平面内做半径为R的匀速圆周运动，设重力加速度为g，则下列说法正确的是（）

　　

　　

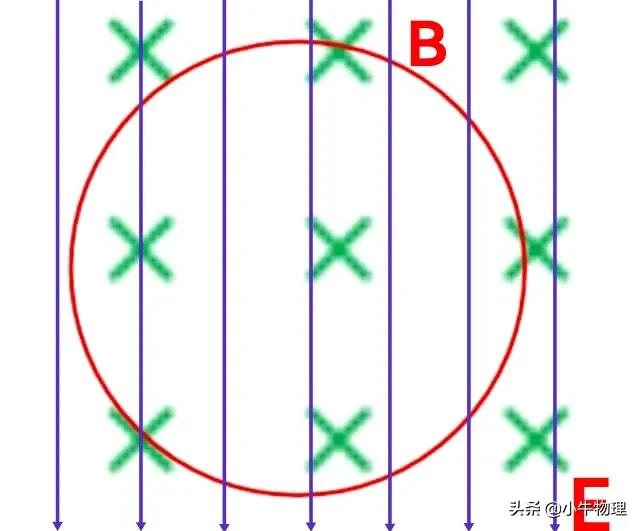
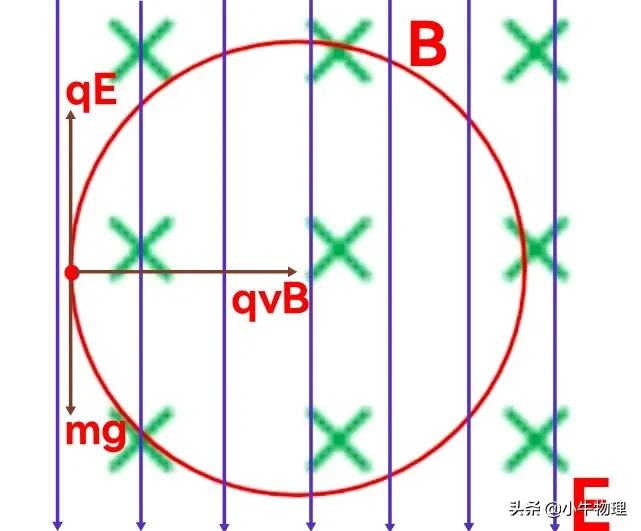
　　A.粒子带负电，且q＝m/E

　　B.粒子顺时针方向转动

　　C.粒子速度大小为V＝BRg/E

　　D.粒子的机械能守恒

　　例题：在如图所示的直角坐标系中，坐标原点O处固定有正点电荷，另有平行于y轴的匀强磁场。一个质量为m，带电量＋q的微粒，恰能以y轴上O′（0，a，0）点为圆心作匀速圆周运动，其轨迹平面与xOz平面平行，角速度为ω，旋转方向如图中箭头所示。试求匀强磁场的磁感应强度大小和方向。

　　

　　

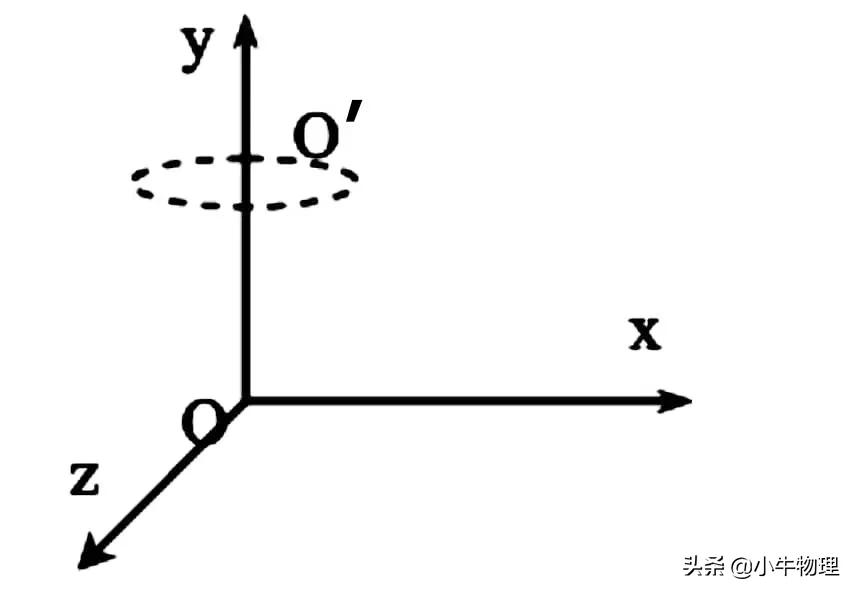
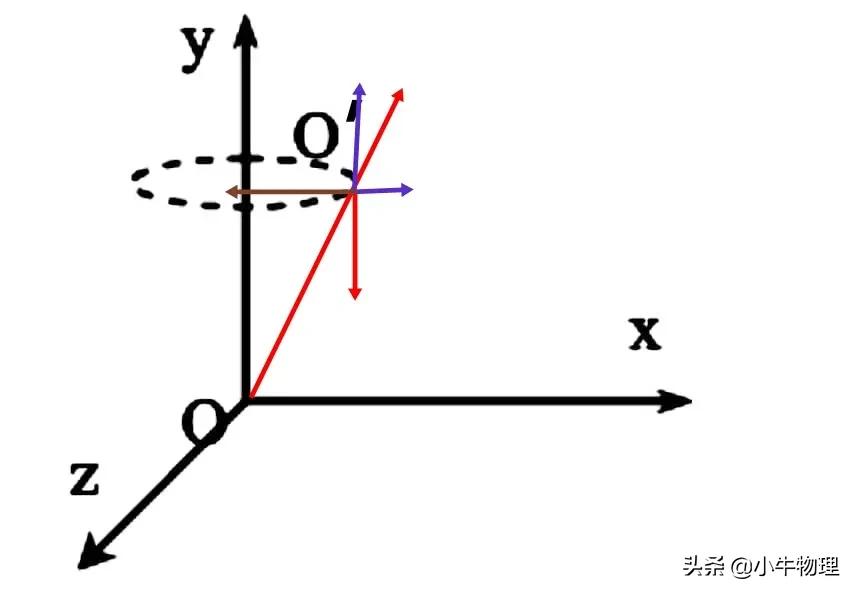
　　③带电粒子在复合场中做平抛或类平抛运动

　　1.【洛伦兹力和电场力抵消】例题：如图所示，匀强磁场的磁感应强度为B，方向竖直向上，将质量为m的带电量为＋q的小球以初速度为v?水平抛出，设外加匀强电场的电场强度为E，方向垂直纸面向里.

　　

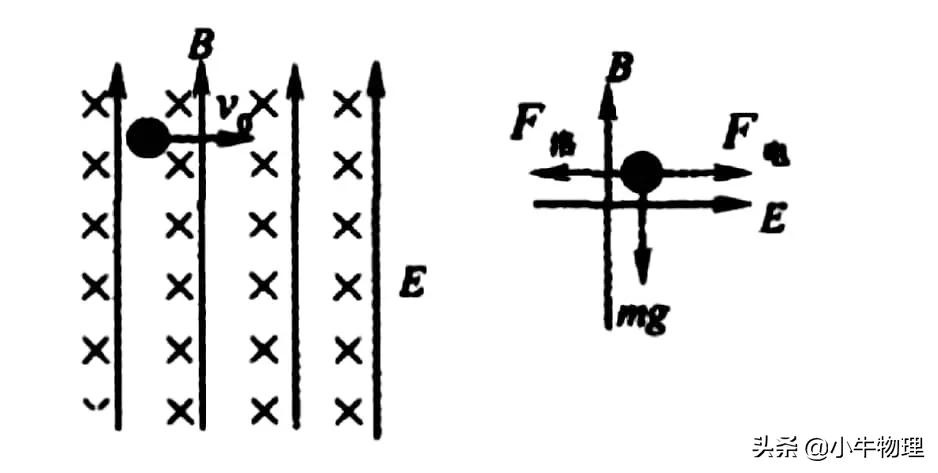
　　解析：由左手定则可知，小球在水平垂直纸面向外受洛伦兹力作用，大小为F＝qv?B，在垂直纸面向里受电场力作用，大小为F＝qE，竖直向下受重力作用，G＝mg，如图所示（左视图），若qv?B＝qE，即水平方向合力为0，速度保持不变，竖直向下只受重力，则加速度为重力加速度g，因此小球做竖直方向的平抛运动，竖直速度增加，但对洛伦兹力无影响.若小球带负电，则洛伦兹力、电场力均反向，情况同上.

　　2.【洛伦兹力和重力抵消】例题：如图所示，匀强磁场的磁感应强度为B，方向垂直纸面向里，将质量为m的带电量为＋q的小球以初速度为v?水平抛出，设外加匀强电场的电场强度为E，方向垂直纸面向外.

　　

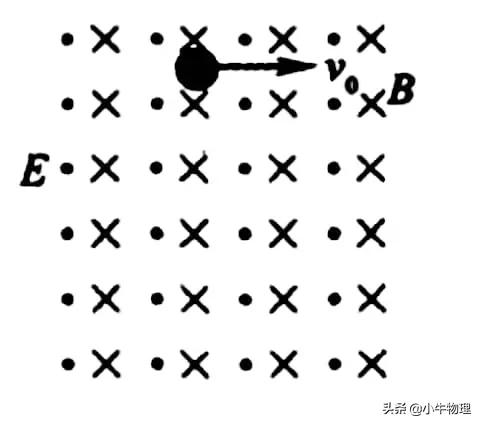
　　解析：由左手定则可知，小球在竖直向上受洛伦兹力作用，大小为F洛＝qv?B，在垂直纸面向外受电场力作用，大小为F＝qE，竖直向下受重力作用，G＝mg，如图所示（左视图），

　　

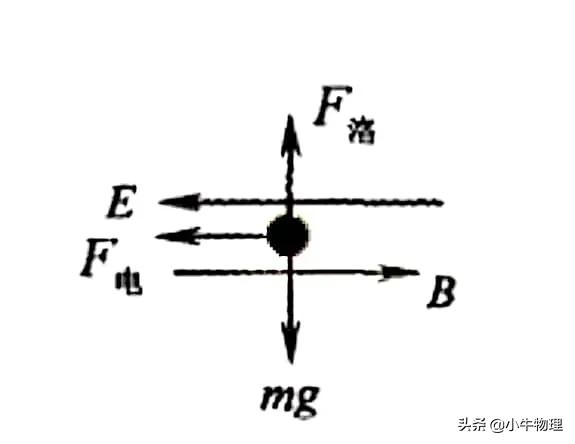
　　若qv?B＝mg，即竖直方向合力为0，速度保持不变，水平方向只受电场力qE，则加速度为重力加速a＝qE/m，因此小球水平向外做平抛运动，垂直于纸面向外速度增加，但对洛伦兹力无影响.

　　当小球带负电时，匀强磁场方向必须垂直纸面向外且满足qv?B＝mg，则小球垂直纸面向里做平抛运动.

　　④带电粒子在具有约束情况下的运动.

　　带电体在复合场中受轻杆、支撑面、轻绳、圆环、轨道等约束的情况下，常见的运动形式有直线运动、圆周运动和类平抛运动.洛伦兹力永不做功，一般用动能定理和牛顿第二定律求解.

　　例题：如图所示，带负电的小球，用一绝缘细线悬挂起来，在一匀强磁场中摆动，匀强磁场的方向垂直纸面向里，小球在A、B间摆动过程中，由A摆到最低点C时，摆线拉力的大小为F?，小球加速度大小为a?，由B摆到最低点C时，摆线拉力的大小为F?，小球加速度大小为a?，则（）.

　　

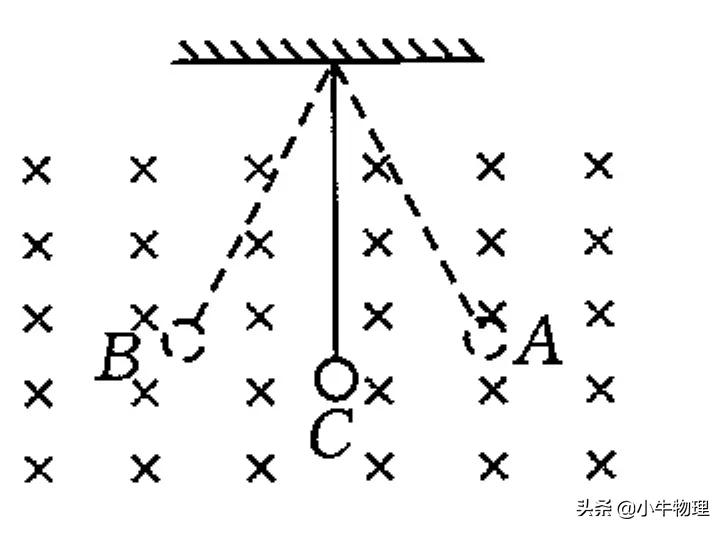
　　A.F?＜F?，a?＝a?

　　B.F?＞F?，a?＝a?

　　C.F?＞F?，a?＞a?

　　D.F?＜F?，a?＜a?

　　例题：如图，绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场，电场方向水平向右，电场强度大小为E，磁场方向垂直纸面向外，磁感应强度大小为B。一质量为m、电荷量为q的带正电的小滑块从A点由静止开始沿MN下滑，到达C点时离开MN做曲线运动。A、C两点间距离为h，重力加速度为g.

　　

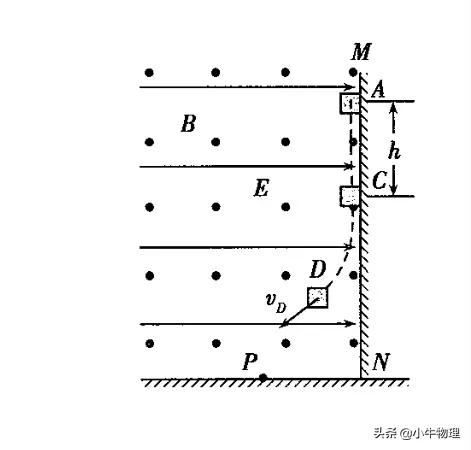
　　（1）求小滑块运动到C点时的速度大小vc；

　　（2）求小滑块从A点运动到C点过程中克服摩擦力做的功Wf；

　　（3）若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置，当小滑块运动到D点时撤去磁场，此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为v?，从D点运动到P点的时间为t，求小滑块运动到P点时速度的大小vp.

　　

　　例题：如图所示，光滑绝缘的半圆形圆弧轨道ACD，固定在竖直面内，轨道处在垂直于轨道平面向里的匀强磁场中，半圆弧的直径AD水平，圆弧的半径为R，匀强磁场的磁感应强度为B，在A端由静止释放一个带正电荷、质量为m的金属小球甲，结果小球甲连续两次通过轨道最低点C时，对轨道的压力差为△F，小球运动过程始终不脱离轨道，重力加速度为g。求：

　　

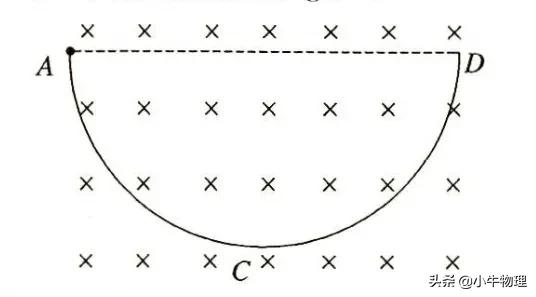
　　（1）小球甲经过轨道最低点C时的速度大小；

　　（2）小球甲所带的电荷量；

　　（3）若在圆弧轨道的最低点C放一个与小球甲完全相同的不带电的金属小球乙，让小球甲仍由轨道的A端由静止释放，则甲球与乙球发生弹性碰撞后的一瞬间，乙球对轨道的压力（不计两球间静电力的作用）。

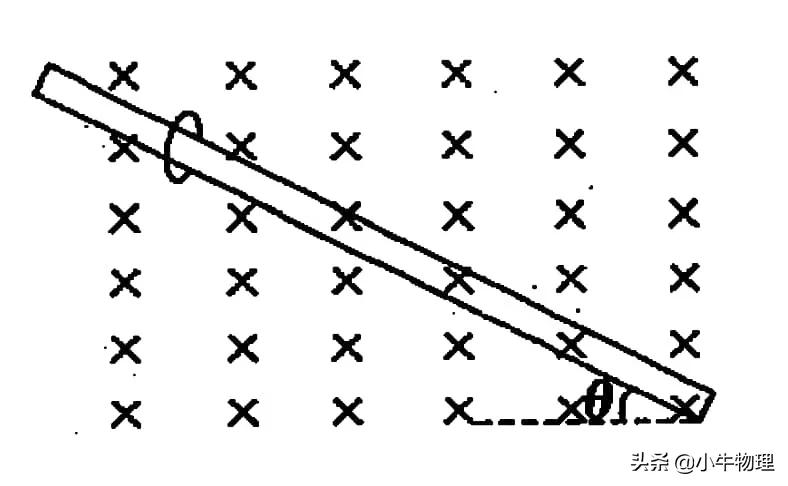
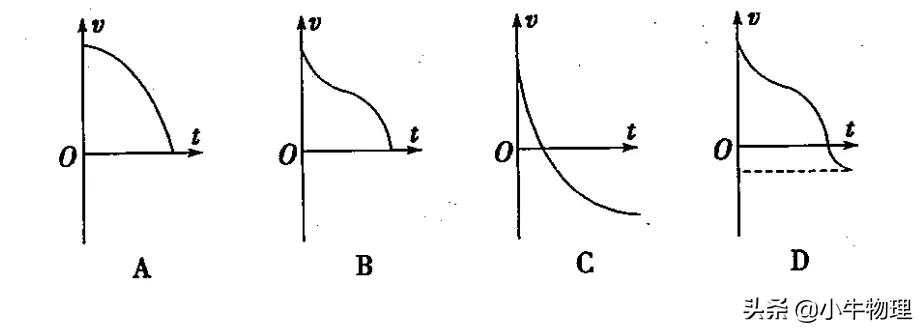
　　例题：一质量为m、电荷量为-q的圆环，套在与水平面成θ角的足够长的粗糙细杆上，圆环的直径略大于杆的直径，细杆处于磁感应强度为B的匀强磁场中，磁场方向水平且垂直于杆.现给圆环一沿杆向上的初速度v?（取初速度v?的方向为正方向），以后的运动过程中圆环运动的速度图象可能是（ABD）

　　

　　

　　⑤带电粒子所受合力大小、方向都在变化，做一般曲线运动，轨迹不是圆，也不是抛物线，而是滚轮线.

　　解题方法有：

　　⒈动能定理

　　⒉牛顿第二定律

　　⒊配速法

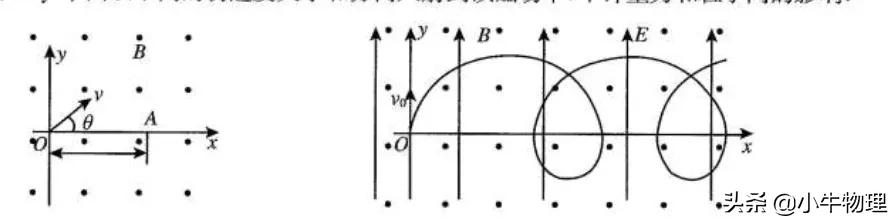
　　例题：如图所示，空间存在一范围足够大的垂直于xOy平面向外的匀强磁场，磁感应强度大小为B.让质量为m，电量为q（q＞O）的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向人射到该磁场中.不计重力和粒子间的影响.

　　（3）如图所示，若在此空间再加入沿y轴正向、大小为E的匀强电场，一粒子从O点以初速度v?沿y轴正向发射.研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量v?，与其所在位置的y坐标成正比，比例系数与场强大小E无关，求该粒子运动过程中的最大速度v?

　　

　　例题：如图所示，空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场。一带电粒子在电场力和洛伦兹力共同作用下，从静止开始自a点沿曲线acb运动，到达b点时速度为零，C点为运动的最低点，不计重力及空气阻力，则（BC）

　　A.粒子必带负电

　　B.a、b两点位于同一高度

　　C.粒子在c点速度最大

　　D.粒子到达b点后将沿原曲线返回

　　声明：本站所有文章，本站所有资源收集于互联网和网友投稿提供，仅用于学习和研究，若用于违法，与本站无关。若有侵权，请联系客服删除。