知识点1 反比例函数图象的画法

　　1.描点法画 图象的一般步骤

　　(1)列表：反比例函数自变量的取值范围是所有

　　(2)描点：以自变量x的取值为

　　 

　　(3)连线：按从左到右的顺序用平滑的曲线连接各点，双曲线的两个分支是

　　划重点

　　画反比例函数图象的特点

　　①反比例函数中自变量x≠0，则y≠0，反比例函数的图象的两个分支都无限地接近但永远不能达到x轴和y轴，所以图象与x轴、y轴没有交点.

　　②画实际问题中的反比例函数图象时应注意自变量的取值范围，它可能是单支，也可能是双曲线的一部分.

　　2.

　　对于同一个非零实数x， 与 的函数值互为相反数，因此函数与(k为常数，k≠0)的图象关于x轴对称.

　　

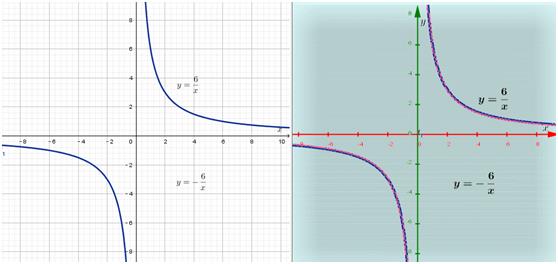
　　3. 反比例函数的图象

　　反比例函数 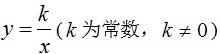图象是由两支分别位于两个象限内的两条曲线组成的，这两支曲线称为双曲线.例如：

　　

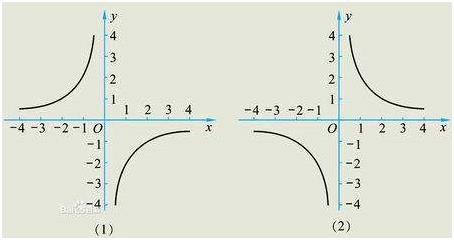
　　拓展

　　双曲线是关于原点成中心对称的图形， 对称中心是原点，它也是轴对称图形，对称轴是直线y=x和y=－x.

　　 

　　示范例题

　　(单选题)[2020广东珠海香洲区期末]函数 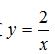的图象大致是(　　)

　　

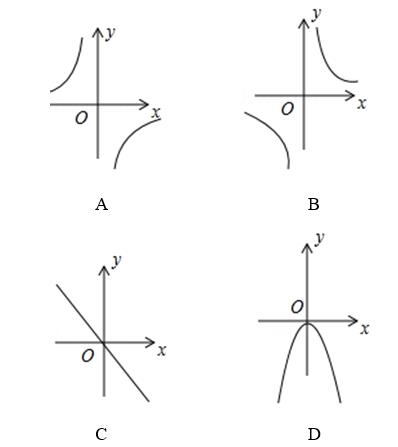
　　A.A

　　B.B

　　C.C

　　D.D

　　【答案】B

　　【解析】根据反比例函数图象的画法，描点画图可知应选B.

　　 

　　知识点2 反比例函数的图象和性质

　　 

　　1. 反比例函数的图象和性质列表如下：

　　

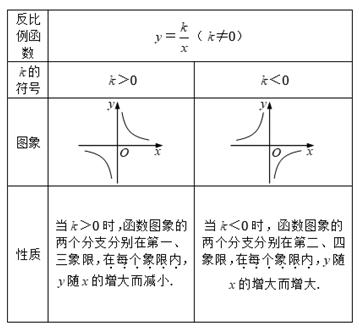
　　反比例函数的增减性

　　(1)反比例函数图象的位置和函数的增减性是由比例系数k的符号决定的，反过来，由双曲线所在的位置和函数的增减性，也可以判断k的符号情况.

　　(2)反比例函数的增减性不是连续的，它的增减性都是在各自的象限内的增减情况.

　　2. 反比例函数的函数值的比较

　　要比较反比例函数的函数值的大小，要特别注意判断所给自变量的值是否是图象同一个分支上的点的横坐标.

　　(1)若给出的自变量的值是同一个分支上的点的横坐标，要根据反比例函数中y随x的增减变化来确定；反之亦然.

　　(2)若不在同一分支上，要根据y的正负来比较大小

　　示范例题

　　例题1.(单选题)[2020辽宁沈阳沈河区月考]在反比例函数 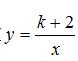图象的每一支曲线上，y都随x的增大而减小，则k的取值范围是（ ）

　　

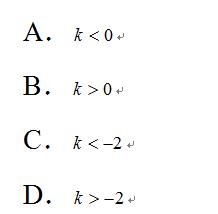
　　【答案】D

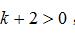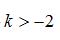　　【解析】根据题意得 ， 解得．故选D．

　　知识点3 反比例函数中k的几何意义

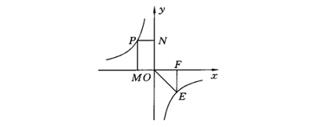
　　1. 过图象任一点作坐标轴垂线，与坐标轴围成的矩形面积

　　如图所示，过双曲线 上的任意一点P(x,y)作x轴 y轴

　　的垂线PM，PN.

　　

　　

　　 

　　

　　 

　　 

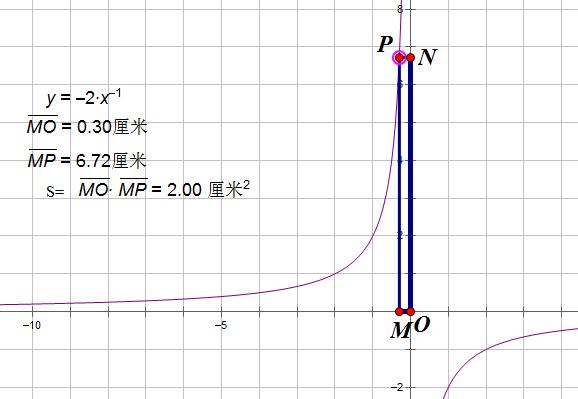
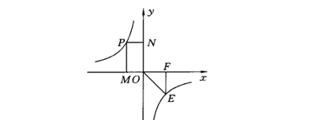
　　2. 过图象任一点作某一坐标轴垂线并连结该点与原点，围成的三角形面积

　　

　　

　　划重点

　　(1) 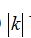可以看作是矩形的面积，并且只要函数式已经确定，不论图象上点的位置如何变化，这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的．

　　(2)已知反比例函数可求矩形面积，反之，已知矩形面积可求反比例函数，此时如果没有指明反比例函数图象的位置，k的值往往存在两种情况.

　　示范例题

　　例题1.(单选题)如图，在 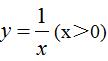的图象上有三个点A，B，P，过这三个点分别向x轴引垂线，交x轴于C，D，E三点，连接OA，OB，OP，设ΔOAC，ΔOBD，ΔOPE的面积分别为S1，S2，S3，则有( )

　　

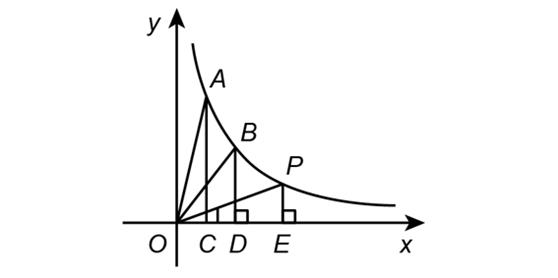
　　A.S1=S2=S3

　　B.S1＜S2＜S3

　　C.S1＞S2＞S3

　　D.S2＞S1＞S3

　　

　　 

　　要点1 函数图象共存问题

　　 

　　解决函数图象共存问题有两种思路：

　　(1)根据函数表达式分析图象

　　比如对于反比例函数与一次函数，可以先假设反比例函数中的比例系数为正(负)，判断对应的一次函数图象经过的象限，再对照选项进行确认或者排除.

　　(2)根据选项分析函数表达式中有关系数

　　判断函数图象是否共存时，先利用其中一个函数图象确定待定字母的取值范围，然后利用函数图象的分布特征进行判断.

　　示范例题

　　例题1.(单选题)[2020河北邯郸复兴区二模] 若 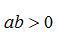，则正比例函数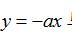与反比例函数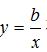在同一平面直角坐标系中的大致图象可能是(　　)

　　

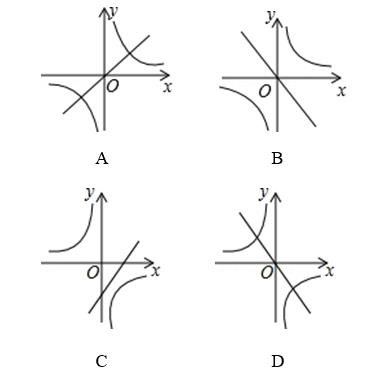
　　A.A

　　B.B

　　C.C

　　D.D

　　

　　要点2 反比例函数与一次函数图象的交点问题

　　1.反比例函数与正比例函数图象的交点

　　设反比例函数y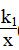＝(k1≠0)，正比例函数y＝k2x(k2≠0)，则

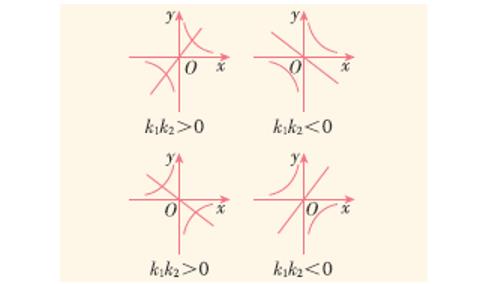
　　(1)当k1k2>0时，两函数图象有两个关于原点对称的交点；

　　(2)当k1k2<0，两函数图象有0个交点.

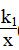　　函数y＝和y＝k2x图象可能的情况如下图.

　　

　　2. 反比例函数与一次函数图象的交点

　　设反比例函数为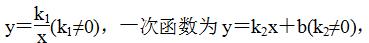

　　

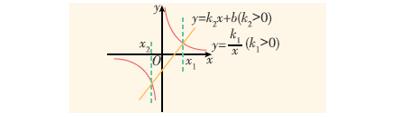
　　3. 根据反比例函数与一次函数图象解不等式

　　

　　示范例题

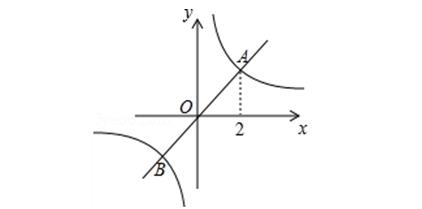
　　例题1.(单选题)[2020广东广州中考数学训练(一)]如图，正比例函数 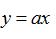的图象与反比例函数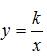的图象相交于A，B两点，其中点A的横坐标为2，则不等式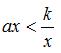的解集为(　　)

　　

　　

　　

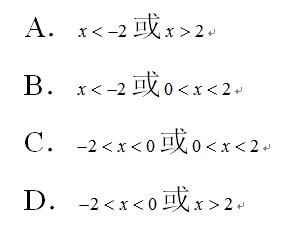
　　声明：本站所有文章，本站所有资源收集于互联网和网友投稿提供，仅用于学习和研究，若用于违法，与本站无关。若有侵权，请联系客服删除。