数学直观是数学核心素养的重要组成部分，数学直观是以“几何图形”为载体，借助于几何图形的形象关系抽象出数量关系，用于计算求值或演绎推理证明，通过演算和推理，不断提高思维的精确性和严密性.以此培养学生严谨的分析问题、解决问题的能力.

　　学生在对勾股定理的研究中会逐渐体会到数形结合思想、方程思想，同时在用面积法验证勾股定理时会用到转化思想(将正方形的面积转化为三角形的面积来求).

　　《周髀算经》介绍了勾股定理及其在测量上的应用，三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，并创制了一幅“勾股圆方图”也叫“赵爽弦图”，利用几何图形的截、割、补、拼来证明代数式之间的恒等关系，给出了勾股定理的详细证明.此图具有严密性、直观性的特点，为我国古代以形证数，形数统一，代数和几何紧密结合、互不可分的独特风格树立了一个典范.本题以“赵爽弦图”为载体，考查了正方形的性质和完全平方公式等知识，渗透了数形结合的数学思想.

　　一、互逆命题与互逆定理

　　1.互逆命题：如果两个命题的题设和结论正好相反，那么这样的两个命题叫做互逆命题，如果把其中一个叫做原命题，那么另一个叫做它的逆命题.

　　2.互逆定理：如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，称这两个定理互为逆定理，其中一个定理称为另一个定理的逆定理.

　　3.互逆命题与互逆定理间关系：(1)命题有真有假，而定理都是真命题.

　　(2)每个命题都有逆命题，但不是所有的定理都有逆定理.

　　例1.下列命题的逆命题是真命题的是?(　　)

　　A.两条直线平行，内错角相等

　　B.如果两个实数相等，那么它们的平方相等

　　C.如果两个实数相等，那么它们的绝对值相等

　　D.全等三角形的对应角相等

　　二、勾股定理的逆定理

　　1.勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形.

　　2.解题步骤：(1)先比较a，b，c的大小，找出最大边长；(2)计算两较小边长的平方和以及最大边长的平方；

　　(3)比较计算结果，若相等，则是直角三角形，并且最长边所对的角是直角；若不相等，则不是直角三角形.

　　勾股定理的逆定理通常用来判断直角三角形或证明线段的垂直关系.

　　

　　例2.△ABC中，AB=7，BC=24，AC=25.在△ABC内有一点P到各边的距离相等，则这个距离为?(　　)

　　A.1　　　　　 B.2　　　　　 C.3　　　　　 D.4

　　例3.某三角形两边的长为4和5,要使该三角形为直角三角形，则第三边长为(　　)

　　A.3　　　　　 B. √41 C.√41或3　　　　　 D.不确定

　　例4.已知Rt△ABC中，∠C=90°,若a+b=14 cm,c=10 cm,则S△ABC为?(　　)

　　A.24 cm2　　　 B.36 cm2　　　 C.48 cm2　　　　 D.60 cm2

　　以下内容为付费内容57%

　　三、常见勾股数

　　1.勾股数：满足a2+b2=c2的三个正整数，成为勾股数，勾股数扩大相同倍数后，任然是勾股数.

　　2.常见勾股数：3，4，5；6，8，10；5，12，13；7，24，25；8，15，17.

　　四、勾股定理逆定理常见运用

　　1.勾股定理逆定理判定直角三角形形状的方法

　　（1）先确定最长边，算出最长边的平方；

　　（2）计算另两边的平方和；

　　（3）比较最长边的平方与另两边的平方和是否相等，若相等，则三角形为直角三角形.

　　例5.在△ABC中,BC=a,AC=b,AB=c,a,b,c互不相等,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).

　　(1)当△ABC三边长分别为6、8、9时,△ABC为　　 三角形;当△ABC三边长分别为6、8、11时,△ABC为　　　 三角形;

　　(2)猜想:当a2+b2　　　 c2时,△ABC为锐角三角形;当a2+b2　　　 c2时,△ABC为钝角三角形;

　　(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.

　　总结：（1）若a2+b2>c2，三角形为锐角三角形;

　　（2）若a2+b2=c2，三角形为直角三角形;

　　（3）若a2+b2<c2，三角形为钝角三角形.

　　2.利用勾股定理逆定理求不规则图形的面积方法

　　（1）作出适当的辅助线将不规则图形分割成面积可求部分及一个三边已知的三角形；

　　（2）利用勾股定理逆定理证明该三角形为直角三角形；

　　（3）求出该直角三角形的面积求出原图形的面积.

　　3.证明线段平方和关系

　　（1）利用平移、旋转、对称等全等变换将需证明的三条线段转移到同一三角形中；

　　（2）利用角度关系证明该三角形为直角三角形；

　　（3）利用勾股定理得出线段平方和关系.

　　

　　4.数形结合解决无理不等式或无理式最值问题

　　（1）将所需表示的无理式表示成 勾股数的平方和形式；

　　（2）将表示无理数的线段在平面适当组合；

　　（3）利用三角形三边关系证明无理数不等式或两点之间线段最短求出无理式最值.

　　5.解决图形翻折问题

　　（1）首先分清图形折叠前后关系；

　　（2）将翻折中得到的直角三角形三边长度求出或用未知数表示出来；

　　（3）利用勾股定理逆定理列出方程，求出未知数的值.

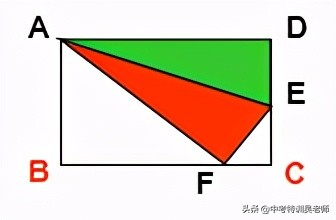
　　例6.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求CF 和EC。

　　

　　6.求立体图形表面爬行最短路径

　　（1）将立体图形侧面展开到一个平面中；

　　（2）利用两点之间线段最短在展开的平面中找到最短路径；

　　（3）利用勾股定理求出最短路径.

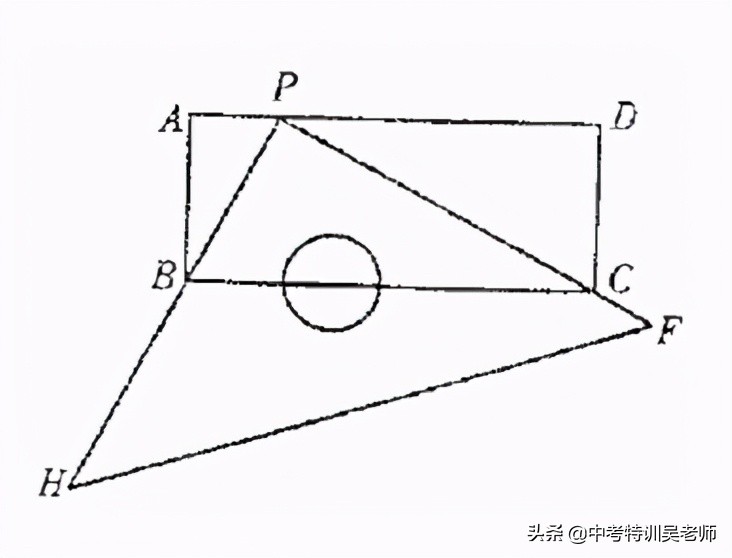
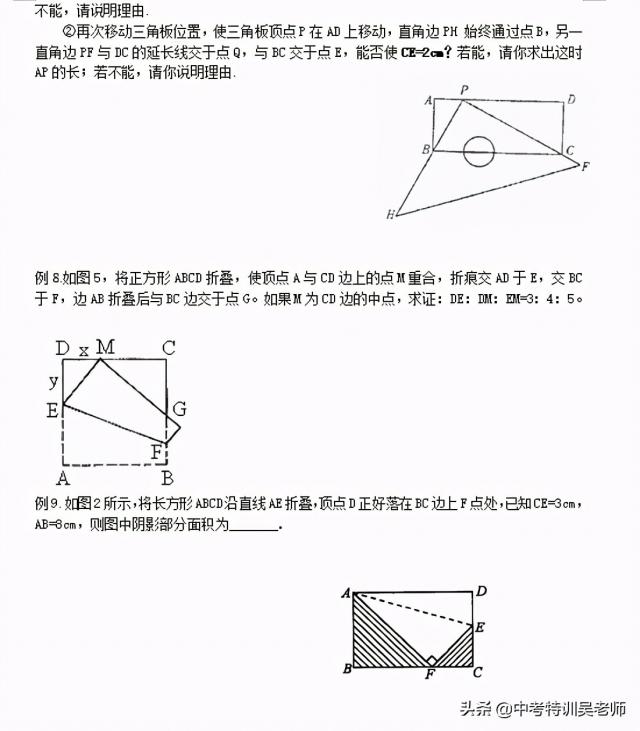
　　例7.如图，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上（不与A、D重合），在AD上适当移动三角板顶点P：

　　①能否使你的三角板两直角边分别通过点B与点C？若能，请你求出这时 AP 的长；若不能，请说明理由.

　　②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH 始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE=2cm？若能，请你求出这时AP的长；若不能，请你说明理由.

　　

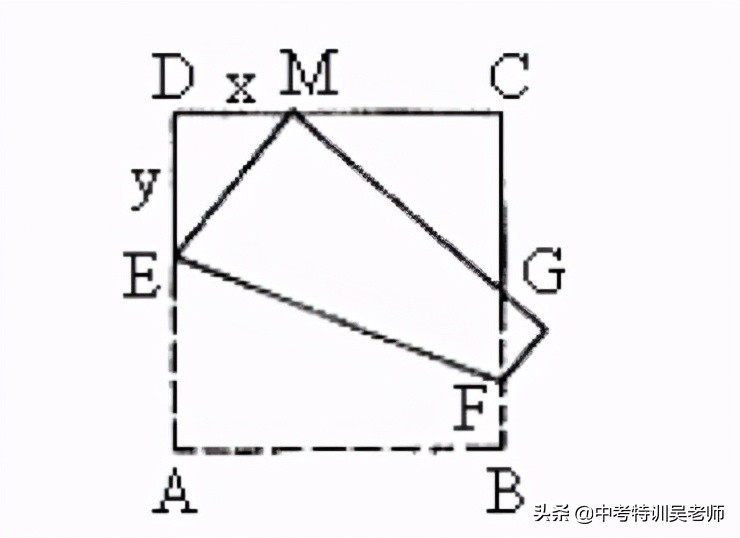
　　例8.如图5，将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G。如果M为CD边的中点，求证：DE：DM：EM=3：4：5。

　　

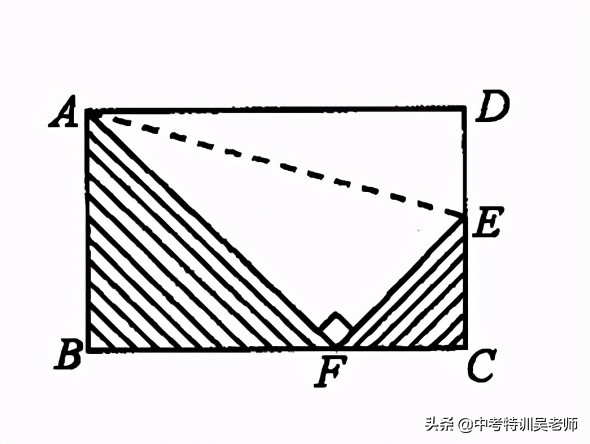
　　例9.如图2所示，将长方形ABCD沿直线AE折叠，顶点D正好落在BC边上F点处，已知CE=3cm，AB=8cm，则图中阴影部分面积为_______．

　　

　　声明：本站所有文章，本站所有资源收集于互联网和网友投稿提供，仅用于学习和研究，若用于违法，与本站无关。若有侵权，请联系客服删除。